Menü

Çokgenler

Çokgenler konusu kpss geometri konuları içinde genelde dörtgenlerle beraber işlenen bir konudur. Ancak çokgenler ve dörtgenler konusunu ayrı ayrı işleyeceğiz. Çokgenler ve dörtgenlerle iligli son 12 yılda 12 tane soru çıkmıştır. Yani kpss genel yetenek kısmında bu konuyla ilgili hemen hemen her yıl bir soru sormaktadır. Sanırım bu istatistikler konunun önemini yeterince ortaya koymaktadır. Çokgen konusunu tamamladıktan sonra bir sonraki konu dörtgenler olacaktır.

Çokgenler

Düzlemde herhangi üçü doğrusal olmayan üç ya da daha fazla noktanın ikişer ikişer birleştirilmesiyle beraber oluşan kapalı geometrik şekillere çokgen denilmektedir. Kpss geometri dersinde kenar sayılarına göre adlandırılan çokgenler, üçgen, dörtgen, beşgen, altıgen … gibi değişik kenar sayılarına göre isimler alır.

kpss çokgen çeşitleri Sırasıyla üçgen, dörtgen, beşgen ve altıgen.

 

kpss çokgen

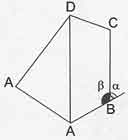
α= Dış Açı.

β= İç Açı.

[AD]= Köşegen: Çokgende komşu olmayan iki köşeyi birleştiren doğru parçasına çokgen denilmektedir.

 

* n Kenarlı Konveks (Dış Bükey) Bir Çokgenin Özellikleri:

  • İç açılar toplamı 180 derecedir. (n-2)
  • Dış açılar toplamı her zaman sabittir ve 360 derecedir.
  • Tüm iç ve dış açılar toplamı n.180 derecedir.
  • Köşegen sayısı formülü: \frac{{n(n - 3)}}{2}
  • Bir köşeden (n-3) köşegen çizilir. Bunlar (n-2) tane üçgen oluşturmaktadır.

Düzgün Çokgen

kpss düzgün çokgen

Tüm kenarları ve tüm iç açıları eş olan dış bükey çokgene düzgün çokgen denir.

Düzgün çokgenin bir dış açısı: \alpha = \frac{{{{360}^ \circ }}}{n}

Düzgün çokgenin bir iç açısı: \beta = \frac{{(n - 2){{.180}^ \circ }}}{n}

Düzgün Beşgen

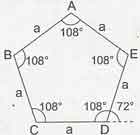
kpss düzgün beşgen

Düzgün beşgenin bir dış açısı: \frac{{{{360}^ \circ }}}{5} = {72^ \circ }

Düzgün beşgenin bir iç açısı: {180^ \circ } - {72^ \circ } = {108^ \circ }

 

kpss düzgün beşgen simetri

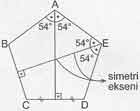
Kpss geometri dersinde Kenar sayısı tek olan beşgen, yedigen, dokuzgen gibi düzgün çokgenlerde bir açıdan karşı kenara indirilen dikme düzgün çokgenin simetri ekseni olmaktadır. Simetri ekseni aynı zamanda bir çokgende yükseklik, kenarortay ve açıortay görevi de yapmaktadır.

 

Düzgün Altıgen

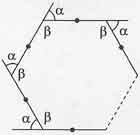
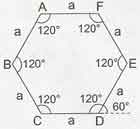
kpss düzgün altıgen

Düzgün altıgenin dış açısı: \frac{{{{360}^ \circ }}}{6} = {60^0}

Düzgün altıgenin iç açısı: {180^ \circ } - {60^ \circ } = {120^ \circ }

 

 

kpss düzgün altıgen simetri

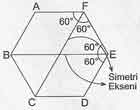
Kenar sayısı altıgen, sekizgen gibi çift olan düzgün çokgennlerde karşılıklı köşeleri her iki tarafında eşit sayıda kenar kalacak şekilde birleştiren doğru simetri eksenidir.

 

 

kpss altıgen alanı

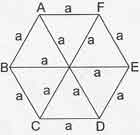
Düzgün altıgenin tüm simetri eksenleri çizilirse, düzgün altıgen 6 tane eşkenar üçgene ayrılır. Böylece ; A(ABCDEF) = 6.\frac{{{a^2}.\sqrt 3 }}{4} sonucu ortaya çıkmaktadır.

 

Kpss genel yetenek geometri dersine ait çokgenler konusu tamamlanmıştır. Bir sonraki kpss geometri konusu dörtgenler olacaktır.

, , , ,

6 Yorum Yapılmış Çokgenler

  1. YasuriSan 11 Ocak 2019 at 22:36 #

    Sekizgenin 5 tane koşegeni vardır.

    Cevapla
  2. Tan 14 Nisan 2015 at 19:42 #

    konu paylaşımınız için teşekkürler

    Cevapla
  3. Cansu 03 Mart 2015 at 22:30 #

    bir köşesinden n-3 formülünden 8-3=5 köşegen
    üçgen ise n-2 den 6 tane

    Cevapla
  4. aygun 22 Şubat 2015 at 19:39 #

    n.(n-3)/2 den 8.(8-3)/2 = 20 köşegen çizilir

    Cevapla
  5. Sıla 22 Aralık 2014 at 19:12 #

    ben şunu diyorum sekizgenin bir köşesinden kaç köşegen çizilir ve kaç üçgen oluşur

    Cevapla
    • Erinç 24 Aralık 2014 at 15:57 #

      sonsuz sayıda mı?

      Cevapla

Bir Cevap Yazın