Özel üçgenler kpss geometri konusu içinde önemli bir yer kaplamaktadır. Üçgenlerle ilgili Kpss’de çıkan soruların çoğunda özel üçgenlerle ilgili teoremler ön plana çıkmaktadır. Özel üçgenler konusu dik üçgen, ikizkenar üçgen ve eşkenar üçgen olarak işlenecektir. Genelde teoremleri ya da formülleri ezbere dayalı olsa da, geometri sorularını çözerken mantık da ön plana çıkmaktadır. Konuyla ilgili bol soru çözümüyle beraber formüller daha rahat akılda kalmaktadir. Ayrıca bol soru çözümüyle özel üçgenler ile ilgili kpss soru tiplerini de daha rahat kavrayabilirsiniz.
Özel Üçgenler
Kpss geometri Özel üçgenler konusu dik üçgen, ikizkenar üçgen ve eşkenar üçgen olmak üzere üçe ayrılır. İlk olarak Dik üçgen, pisagor teoremi ve öklid teoremi ile başlayalım.
Dik Üçgen
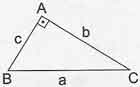 Özel üçgenler içinde yer alan Dik üçgen, bir açısı dik olan üçgenlere denir. Dik üçgende en uzun kenara hipotenüs denir. Diğer kenarlara da dik kenarlar denir.
Özel üçgenler içinde yer alan Dik üçgen, bir açısı dik olan üçgenlere denir. Dik üçgende en uzun kenara hipotenüs denir. Diğer kenarlara da dik kenarlar denir.
* Dik Üçgenin Özellikleri:
Kpss geometri dersine ait dik üçgenin birçok özelliği bulunmaktadır. Bu özelliklerin içinde pisagor teoremi ve öklid teoremi de yer almaktadır. Şimdi bu özellikleri sıralayalım.
Bu teoreme göre hipotenüsün karesi, diğer dik kenarların karesinin toplamına eşittir. Kpss geometri sorularında genelde kullanılan bazı dik üçgen katları vardır. Bunlar;
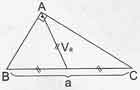 Muhteşem Üçlü: Bir dik üçgende hipotenüse ait kenarortay uzunluğu hipotenüsün yarısına eşittir. Buna geometri dersinde muhteşem üçlü denir.
Muhteşem Üçlü: Bir dik üçgende hipotenüse ait kenarortay uzunluğu hipotenüsün yarısına eşittir. Buna geometri dersinde muhteşem üçlü denir.
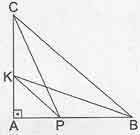
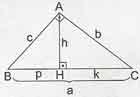 Öklid Teoremi: Bu teorem dik üçgenler içinde önemli bir yer kaplamaktadır ve birçok kpss üçgen sorusunun kısa yoldan çözülmesine olanak sağlamaktadır. Öklid teoremi uygulanabilmesi için dik bir üçgende hipotenüse ayrı bir dik (h) inmesi gerekmektedir. Öklid teoremi ile ilgili formüller aşağıda listelenmiştir.
Öklid Teoremi: Bu teorem dik üçgenler içinde önemli bir yer kaplamaktadır ve birçok kpss üçgen sorusunun kısa yoldan çözülmesine olanak sağlamaktadır. Öklid teoremi uygulanabilmesi için dik bir üçgende hipotenüse ayrı bir dik (h) inmesi gerekmektedir. Öklid teoremi ile ilgili formüller aşağıda listelenmiştir.
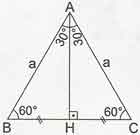
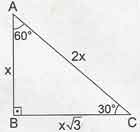 90-60-30 Üçgeni: Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir. 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın
90-60-30 Üçgeni: Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir. 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittir.
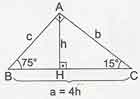 Bir dik üçgende dar açılardan birinin ölçüsü 15 derece ise, hipotenüs uzunluğu hipotenüse ait yüksekliğin 4 katıdır.
Bir dik üçgende dar açılardan birinin ölçüsü 15 derece ise, hipotenüs uzunluğu hipotenüse ait yüksekliğin 4 katıdır.
Özel üçgenler içinde yer alan dik üçgen ile ilgili özellikler tamamlanmıştır. Şimdi özel üçgenler içinde yer alan ikizkenar üçgen konusuna bakalım.
İkizkenar Üçgen
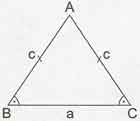 Özel üçgenler içinde, iki kenarı eşit olan üçgenlere ikizkenar üçgen denmektedir. Yandaki ikizkenar üçgene göre;
Özel üçgenler içinde, iki kenarı eşit olan üçgenlere ikizkenar üçgen denmektedir. Yandaki ikizkenar üçgene göre;
A: Tepe noktası
a: Taban uzunluğu
m(A): Tepe açısı olarak adlandırılmaktadır.
- Eşit kenarların karşısındaki açılar eşittir.
- İkizkenar üçgende tabana ait yükseklik, kenarortay ve açıortay uzunlukları eşittir.
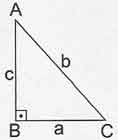
Bir ABC ikizkenar üçgeninde;
Eşkenar Üçgen
Özel üçgenler içinde yer alan eşkenar üçgen tüm kenar uzunlukları eşit olan üçgendir.
- Eşkenar üçgende bütün yükseklik, kenarortay ve açıortay uzunlukları eşittir.
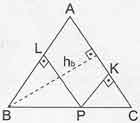
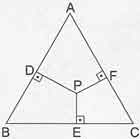
- Bir eşkenar üçgenin iç bölgesinde herhangi bir yerinden alınan bir noktadan, kenarlara inilen dikmelerin toplamı yüksekliğine eşittir.
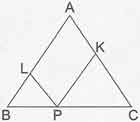
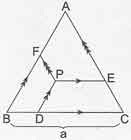
- Kpss genel yetenek geometri dersi özel üçgenler içinde yer alan bir eşkenar ğçgenin içinde alınan herhangi bir P noktasından kenarlara çizilen paralellerin uzunlukları toplamı eşkenar üçgenin bir kenarının uzunluğuna eşittir.
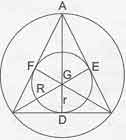
- Bir eşkenar üçgende ağırlık merkezi, çevrel ve içteğet çemberinin merkezi aynı noktatadır. Bu nokta aynı zamanda yüksekliklerin ve iç açıortayların da kesim noktasıdır.
h=3r
R=2r
Kpss genel yetenek geometri dersine ait özel üçgenler ; dik üçgen, ikizkenar üçgen ve eşkenar üçgen konuları tamamlanmıştır. Bir sonraki kpss geometri dersinin konusuÜçgenin Alanı olacaktır.


Şu ana kadarki en yararlı site. Yarınki sınavimda çok yararli oldu.
Beyler türklerin gücünü gösterlim herkes bayrak atsn
Eyvallah cok isime yaradu
ikzkenar üçgende 60 derece olur mu
EŞKENAR ÜÇGENLER AYNI ZAMANDA İKİZKENAR DIR
denizcim eskenar ucgen tum açıları ve kenarları eşit olan üçgenlerdir onun için eşkenar üçgen denir ikizkenar üçgen ise iki kenarı ve acısı esit olan demektir ikisini karıştırma canım
Aysecim her eşkenar üçgen ikizkenar üçgendir ama her ikizkenar üçgen eşkenar üçgen değildir.Denizin dediği doğrudur.
berkaycım eşkenar ucgun artık ikizkenarlıktan cıkıp ucuzkenarlıga dönmüştür o yüzden ikizkenar demesi yanlıştır canım
anlamadım yaa
Harika olmuş çok işime yaraadı çok teşekkürler 🙂
Aynen süperdi.Gerçekten de Ç❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️K güzel olmuş.Çok işime yaradı.? ? ?Sağ olun.Elinize emeğinize bilginize sağlık.? ?Gerçekten de çok emek harcadığınız belli oluyor.? ?Yani aslında tek kelimeyle ?????? olmuş.? ? ?
ama ben eş kenar üçgen çeşitleri istiyordum 🙁
Cok tesekkurler.
Bir ikizkenar üçgende hipotenüs 6 , dik kenarı bulamıyorum yardım eder misiniz?
3 kök iki
18
Kök 18 yani 3 kök iki
Güzel-miş
ciddisin
Hiç işime yaramadı bir ikizkenar ucgenin eğimi verilmişse eğim acisi nasıl bulunur
Çok güzrldi ama hiç bişey anlamadım
aranan mizah 😀
aradığımı bulama yinede çok güzel teşekkürler..
bende beğendim, elinize sağlık
güzelmiş
çok iyi sınava burdan çalıştım 🙂
süperr
çoküzel
konuyu daha iyi anladım ve pojeme de işime yaradı çok sağol’un
çok sağolun
Site güzel ben beğendim
ikizkenar üçgenin açılarını bulmm gerek yardımcı olursanız sevinirim
Gerçekden çok iyi çok işime yaradı emeği geçenlere teşekkürler. 🙂
bu siteyi çok seviyorum
çok güzel işime yaradı (daha doğrusu çocuklarıma)
Çok güzel anlatmışlar iş yerinde bazı hesaplamar yaparken kullandım.
Emeği geçen herkese çok teşekkür ederim geometriyi çözdüm sayenizde
Güzel Valla Emeğinize Sağlık 🙂
süperr
hiç işime yaramadı 😀
çok saçma yaa hiç birşey anlayamadım ben
çok yaradı saol
çok iyi ve yararlı bir şey
gerçekten çok iyi bir site çok işime yaradı
Gerçekden işime çok yaradı çok iyy soru lar pırojeme çok fay dası oldu 🙂
benimde
ayrıntıya inilmemiş ama olmuş……
ödev çok güzel ama içinde soru yok soru olsaydı herkes çok çabuk anlardı
gercekten çok ıyı hazırlanmıs bır konu ..geometrı odevımde cok yardımcı oldu..tesekurler…
emeyi Geçen Herkesden Tek Tek Teşekür Ederim çok iyşime yaradı 🙂
gerçekten teşekkürler ödevi yapmama yardımcı oldu 😀
t€ş€kkürl€r
harikaaaaaaaaaaaaaaaaa çok iyi
gerçekten çok işime yaradı bu site teşekürler
gerçekten harika bir site çok işime yaradı çok teşekkürler
gerçekten muhteşem bir site,hem çok beğendim hem de öğretmenim anlatırcasına anladım.gerçekten çok büyük yardımcı oldu,tekrar teşekkürler. 🙂
gerçekten çok işime yaradı Allah razı olsun emeği geçenlerden 🙂
teşekkürler.
İşime yaradı tesekkurler 🙂
hiçbişey bulamadımmm
dikkatli bakmamışsın
aynen
cok ıyı daha ıyı ders aanlamayı gosterıyorsunuz tesekurler…
ali ozaman aramalıyız 😀 bende bulamadım 😀
O zaman dansss…
Hem performansı yapmama hem de konuyu daha iyi anlamama çok yardımcı oldu.Teşekkürler
bence hiçde yardımcı olmuyor hem sadece konuyu anlatıyor benim sadece dik üçgen resimlerine ihtiyacım var ama konu dişi bişeylerle karşilasıyomm
Emeği geçenlere teşekkürler gerçekten çok yararı oldu 🙂
çok saçma
saçma olan bir şey var o da sensin buse
sende saçmasın
Sana katıliyorum
bulamadım
Cok guzel isime yaradi