Paralelkenar

Paralelkenar bir dörtgen çeşididir. Konumuzda paralelkenar özelliklerini, paralelkenar alan hesaplamaları ile ilgili yöntem ve özellikleri inceleyeceğiz. Paralelkenar konusu kpss geometri dersinin eğlenceli ve soru çözmesi zevkli bir konusudur. Şunu unutmayalım ki geometride en önemli kısım dikkat ve sorudaki özelliği yada isteneni görebilme yeteneğini kazanmaktır. Bu da ancak bol örnek çözmekle ve sık sık tekrar yapmak ile mümkün olmaktadır. Önceki konumuzda Dörtgenleri incelemiştik. Sıradaki konumuz ise Paralelkenar olacaktır.

Paralelkenar

Karşılıklı kenarları birbirine paralel ve eş olan dörtgenlere paralelkenar denir.

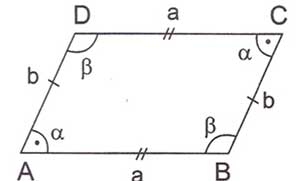$ \displaystyle \left[ AB \right]$//$ \displaystyle \left[ CD \right]$

$ \displaystyle \left[ BC \right]$//$ \displaystyle \left[ AD \right]$

Paralelkenar Özellikleri:

1. Paralelkenarın karşılıklı açıları birbirine eşittir.

2. Paralelkenarın karşılıklı kenarları birbirine eşittir.

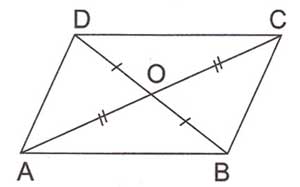
3. Paralelkenarın köşegenleri birbirini ortalar.

$ \displaystyle \left| AO \right|=\left| CO \right|$

$ \displaystyle \left| BO \right|=\left| DO \right|$

Yani bölünen köşegenin her iki parçası birbirine eşittir.

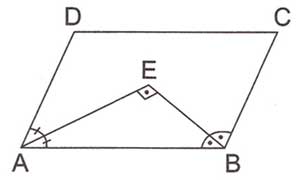
4. $ \displaystyle \left[ AE \right]$ ile $ \displaystyle \left[ BE \right]$ açıortay ise m($ \displaystyle \widehat{AEB}$)=$ \displaystyle {{90}^{0}}$

Açıortayların kesiştikleri bölümdeki açı $ \displaystyle {{90}^{0}}$’dir.

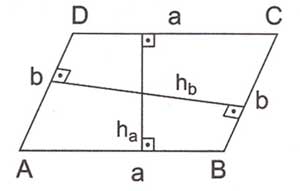
Paralelkenarın Alanı

Alan (ABCD)=a.$ \displaystyle {{h}_{a}}$=b.$ \displaystyle {{h}_{b}}$

Kenar ve o kenarın yüksekliğinin çarpımı  paralelkenarın alanını vermektedir.

a.

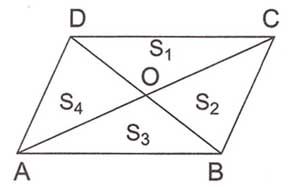
$ \displaystyle {{S}_{1}}$=$ \displaystyle {{S}_{2}}$=$ \displaystyle {{S}_{3}}$=$ \displaystyle {{S}_{4}}$

Köşegenlerle 4’e ayrılmış bir paralel kenarın her bir bölümünün alanı birbirine eşittir.

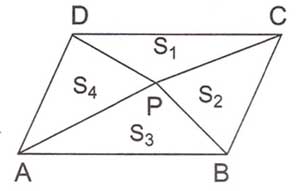
b. “P”, paralel kenar içinde herhangi bir nokta  olsun.

$ \displaystyle {{S}_{1}}$+$ \displaystyle {{S}_{3}}$=$ \displaystyle {{S}_{2}}$+$ \displaystyle {{S}_{4}}$=$ \displaystyle \frac{A(ABCD)}{2}$

Oluşan üçgenlerden karşılıklı olanlarının alanları toplamı paralelkenar alanının yarısına eşittir.

c.
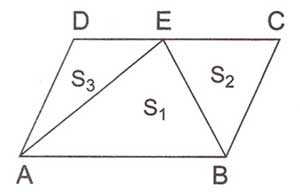$ \displaystyle {{S}_{1}}$=$ \displaystyle {{S}_{2}}$+$ \displaystyle {{S}_{3}}$ ve Alan (AEB)= $ \displaystyle \frac{A(ABCD)}{2}$

Paralel kenar bir kenardan belirlenen herhangi bir tepe noktasından bölünerek üç tane üçgen elde edilir. Şekilde görüldüğü gibi büyük üçgenin alanı diğer iki küçük üçgenin alanlarının toplamına eşittir.

Kpss genel yetenek geometri dersine ait Paralelkenar konusu tamamlanmıştır. Bir sonraki kpss genel yetenek geometri konusu Dikdörtgen olacaktır.