Üçgende açı konusuna geçmeden önce Kpss geometri konusu içinde sık sık karşılaşacağımız üçgen terimini inceleyelim. Üçgen doğrusal olmayan farklı üç tane noktayı birleştiren doğru parçalarının birleşimine denir.
ABC üçgeni bu şekilde tanımlanmaktadır.
Üçgende Açı
Bir üçgende iç açıların toplamı 180° dir. Dış açıların toplamı ise 360° dir.
Üçgende açı konusunda dikkat etmemiz gereken ve forumulize edilmiş birkaç önemli nokta vardır. Şimdi üçgende açı konusunda yer alan bu detayları teker teker inceleyelim.
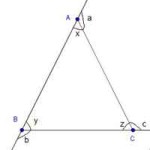 * Bir üçgende bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri toplamına eşittir.
* Bir üçgende bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri toplamına eşittir.
x+y+z=180°
a+b+c=360°
a=y+z
b=x+z
c=x+y
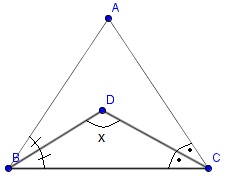 * Bir ABC üçgeninde [BD] ve [CD] iç açıortay, D iç nokta ise;
* Bir ABC üçgeninde [BD] ve [CD] iç açıortay, D iç nokta ise;
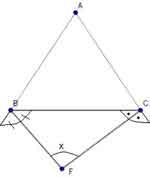 * Üçgende açı konusunda bir ABC üçgeninde [BF] ve [CF] dış açıortay ise;
* Üçgende açı konusunda bir ABC üçgeninde [BF] ve [CF] dış açıortay ise;
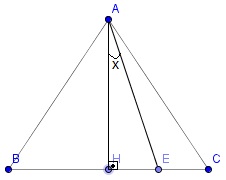
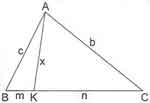
* Bir üçgende şekildeki gibi [AH] yükseklik ise ve [AE] BAC açısının açıortayı ise;
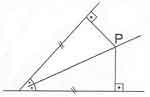
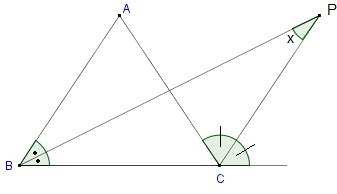 * Bir ABC üçgeninde [BP] iç açıortay, [PC] dış ortay ise;
* Bir ABC üçgeninde [BP] iç açıortay, [PC] dış ortay ise;
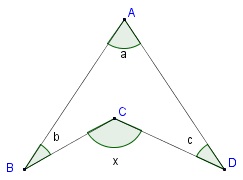
* Üçgende açı konusunda yandaki şekil gibi konkav bir üçgen çıktığında açı formulü şu şekilde olmaktadır;
Kpss genel yetenek ve kpss geometri konuları dahilinde üçgende açı ile ilgili önemli noktalar yukarıda verilmiştir. Şimdi açıortay konusunu inceleyelim.
Açıortay
 Bir üçgende açı kollarına uzaklıkları eşit olan noktaların geometrik yerine açıortay denir. Kpss geometri konuları içerisinde açıortaydan çok fazla soru sormamaktadır. Ancak bu, konuyu bilmememiz gerektiği anlamına gelmez. Çünkü her sene değişik yerden soru sormakta olan Kpss lisans sınavı ters köşe etmeyi çok sevmektedir. Bu yüzden dikkat ederek açıortay konusuna devam edelim.
Bir üçgende açı kollarına uzaklıkları eşit olan noktaların geometrik yerine açıortay denir. Kpss geometri konuları içerisinde açıortaydan çok fazla soru sormamaktadır. Ancak bu, konuyu bilmememiz gerektiği anlamına gelmez. Çünkü her sene değişik yerden soru sormakta olan Kpss lisans sınavı ters köşe etmeyi çok sevmektedir. Bu yüzden dikkat ederek açıortay konusuna devam edelim.
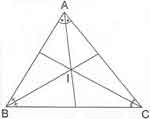 * Bir üçgende iç açıortaylar bir noktada kesişirlerse , bu nokta üçgenin iç teğet çember merkezini oluşturur ve genelde I ile gösterilmektedir.
* Bir üçgende iç açıortaylar bir noktada kesişirlerse , bu nokta üçgenin iç teğet çember merkezini oluşturur ve genelde I ile gösterilmektedir.
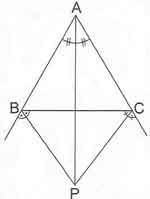 * Bir üçgende iki dış açıortay ile üçüncü iç açıortay bir noktada kesişmektedir.
* Bir üçgende iki dış açıortay ile üçüncü iç açıortay bir noktada kesişmektedir.
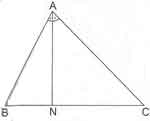 * İç Açıortay Teoremi: [AN] açıortay doğrusu olmak üzere;
* İç Açıortay Teoremi: [AN] açıortay doğrusu olmak üzere;
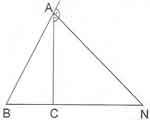 * Dış Açıortay Teoremi: [AN] dış açıortay doğrusu olmak üzere;
* Dış Açıortay Teoremi: [AN] dış açıortay doğrusu olmak üzere;
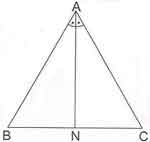 * İç Açıortay Uzunluğu: [AN] iç açıortay doğrusu olmak üzere;
* İç Açıortay Uzunluğu: [AN] iç açıortay doğrusu olmak üzere;
* Dış Açıortay Uzunluğu: [AN] dış açıortay doğrusu olmak üzere; 
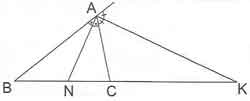 * İç Açıortay ve Dış Açıortay Birlikte: [AN] iç açıortay doğrusu, [AK] dış açıortay doğrusu olmak üzere;
* İç Açıortay ve Dış Açıortay Birlikte: [AN] iç açıortay doğrusu, [AK] dış açıortay doğrusu olmak üzere;
Kenarortay
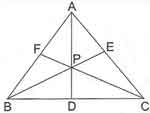
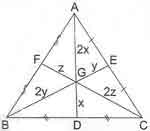 * Bir üçgenin kenarortayları tek bir noktada kesişirse bu noktaya ağırlık merkezi denir ve G ile gösterilir. Kenarortaylar birbirlerini kenarlarına doğru 1, köşeye doğru 2 oranında bölmektedirler.
* Bir üçgenin kenarortayları tek bir noktada kesişirse bu noktaya ağırlık merkezi denir ve G ile gösterilir. Kenarortaylar birbirlerini kenarlarına doğru 1, köşeye doğru 2 oranında bölmektedirler.
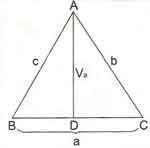 * Kenarortay Teoremi: [AD] uzunluğu kenar ortay olmak üzere;
* Kenarortay Teoremi: [AD] uzunluğu kenar ortay olmak üzere;
formülleri oluşmaktadır. Bu formüllerden şu sonuç çıkmaktadır:
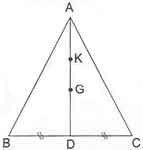 * Bir ABC üçgeninde G ağırlık merkezi ve [AD] uzunluğu kenarortay olmak üzere;
* Bir ABC üçgeninde G ağırlık merkezi ve [AD] uzunluğu kenarortay olmak üzere;
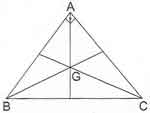 * Bir ABC üçgeninde G ağırlık merkezi ve A açısı 90 derece olmak üzere;
* Bir ABC üçgeninde G ağırlık merkezi ve A açısı 90 derece olmak üzere;
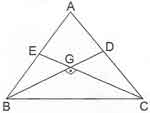 * Bir ABC üçgeninde G ağırlık merkezi ve G açısı 90 derece olmak üzere;
* Bir ABC üçgeninde G ağırlık merkezi ve G açısı 90 derece olmak üzere;
Üçgende Kesenler
1) Menelaus Teoremi:
2) Seva Teoremi:
3) Stewart Teoremi:
4) Carnot Teoremi:

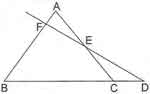
bir üçgenin kenar ortayları üçgenin dışında kesilebilir mi
Hayır. Kenarortaylar her zaman üçgenin iç bölgesinde kesişiyor.
aynen
üçgende kenarortay doğrusu inmek için ikizkenar olması şartmı?
hayır…
Kenarortay ve Açıortay, üçgenin özelliğine bağlı değildir… Kenarortay ve Açıortaylar; her türlü üçgende mevcut olabilir…
tşk
cok iyiymiş sevdim burayı odevime yardımcı oldu
?????????
?????
Vallami la ?
Vallahı da Öğretmen aferım dedi 😀
üçgenler çok zor ama zevkli bir konu
güzel iii ki ödevimde yararlı oldu
sınavın büyük bi bölümünü üçgenler oluşturmakta. yüzden bu konuyu yapmakan başka bi çarem yokkk:(((
Kesinlikle ☆☆☆☆☆
aynen katılıyorum
zaten butun dokuzlarda oyle degil mi
Evet