Taban aritmetiği kpss matematik konuları içinde önemli bir yer teşkil etmektedir. Taban aritmetiği bir sayının hangi rakamlardan oluşacağını ve sayıyı yazarken kullandığımız sayma sistemini belirler. Normal matematik işlemlerinde kullandığımız rakamlar 10’luk sayma sisteminde kullandığımız rakamlardır. Diğer sayma sistemlerinde taban aritmetiği nasıl işliyor kontrol edelim.
Taban Aritmetiği
10’luk sayma sisteminde kullanılan rakamlar : 0,1,2,3,4,5,6,7,8,9
6’lık sayma sisteminde kullanılan rakamlar: 0,1,2,3,4,5
4’lük sayma sisteminde kullanılan rakamlar: 0,1,2,3
Taban aritmetiğinde dikkat edilecek bir diğer nokta da şeklindeki yazılan bir sayı sisteminde t>1, yani tabanın her zaman 1’den büyük olması gerektiğidir. Buradaki sayı sistemini oluşturan rakamlar da a, b ve c her zaman t’den küçük rakamlardır.
- 5 tabanın yazılabilecek üç basamaklı rakamları farklı en büyük sayı kaçtır?
sayısı 5 tabanında rakamları farklı olarak yazılabilecek en büyük sayıdır.
- 9 tabanında dört basamaklı rakamları farklı yazılabilecek en küçük sayı kaçtır?
* Herhangi Bir Tabandaki Sayının 10’luk Tabana Çevrilmesi (Çözümlenmesi):
Kpss matematik taban aritmetiği sorularında bir sayı 10’luk tabana çevrilirken, çevrilecek olan sayı sisteminin taban rakamı (t) ele alınır. Buradaki t 1’ler basamağından başlayarak sırası ile baştaki basama kadar taban rakamının üstleri şeklinde çarpılır. Daha iyi anlayabilmek için aşağıdaki örnekleri inceleyelim.
10’luk tabanda yazılan sayılar bizim normalde matematikte kullandığımız sayılardır. Bu sayıların taban rakamını 10 ile göstermeye gerek yoktur. Çünkü 10’luk tabanda yazıldığı bilinmektedir.
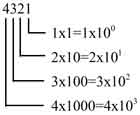
4321 sayısını 10’luk tabana göre çözümlersek;
Burada çarpılan sayıları toplarsak;
1+20+300+4000= 4321 eder. İşten 10’luk tabandaki sayının çözümlenmesi bu şekildedir. Ancak, sayı zaten çözümlenmiş olarak yazılmış vaziyettedir. Bunu gösterme amacımız ise kpss sorularında taban rakamı farklı olduğunda çözümleme için bu yolu izlememizdir.
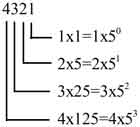
5 tabanında yazılmış bu sayıyı da aynı mantıkla 10’luk tabana çevirerek çözelim;
* 10’luk Tabandaki Bir Sayıyı Herhangi Bir Tabana Çevirme:
10’luk tabanda verilen sayı hangi tabandaki sayıya çevrilecekse ona sürekli bölünür. Sonra en son bölümden başlayarak kalanlar alınır ve sayı bu şekilde oluşturulur.
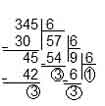
- 345 sayısını 6’lık tabana çevirelim:
Görüleceği üzere 345 sayısını devamlı olarak böldüğümüzde kalanlar sondan başlayarak alınır ve 6 tabanındaki sayı yazılır.
* Taban Aritmetiğinde İşlemler:
- Toplama: Taban aritmetiğinde toplama işlemi yapılırken, rakamlar toplandığında bulunan sonuç tabana eşit ya da tabandan büyük ise sonuç taban bölünür.
- Çıkarma: Çıkarma işleminde de dikkat edilmesi gereken , sıfır çıkarma işleminde hangi tabanda ise onun ismi ile okunur.
3’ten 5 çıkmaz solundan bir 6’lık alırız => 9-5=4 birler basamağına yazılır.
0’dan 4 çıkmaz. sol tarafındaki 5’ten bir 6’lık alınır. 6’dan bir altı önceki işlemde almıştık kaldı 5. => 5-4=1 Onlar basamağına yazılır.
5’ten bir 6’lık almıştık kaldı 4. => 4-2= 2 sonuç 214 olarak karşımıza çıkar.
- Çarpma: Taban aritmetiğinde çarpma işlemi yapılırken toplama işlemi gibi ”kalan” ve ”elde” olanlardan faydalanılır.
* Taban Aritmetiğinde Tek ve Çift Sayılar:
- Taban aritmetiğinde taban çift ise, sayının birler basamağına bakılır. Birler basamağı tek ise sayı tek, çift ise çift sayıdır.
- Taban aritmetiğinde tabank tek ise, sayının rakamları toplamına bakılır. Eğer toplam tek ise sayı tek, toplam çift ise sayı çifttir.
Kpss genel yetenek matematik dersine ait Taban Aritmetiği konusu tamamlanmıştır. Bir sonraki kpss matematik konusu Bölünebilme Kuralları olacaktır.


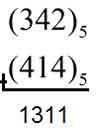
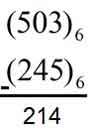
en son örnekteki çift sayıda taban sayının rakamından küçük nasıl oluyor
104-55 6 tabanında kaçtır?,
5
16 sayisi 8 tabaninda yazirlirsa sondan kac basamagi sifir olur?
16 uzeri 5 olcakti ama yapamamisim
6
40 sayfalık bir kitabın sayfaları 5 tabanına göre numaralandırılırsa buna göre bu kitabın sayfaları numaralandırılırken kaç tane rakam kulanılır
Çıkarma işleminde bir hata yok. Onluk tabanı düşünerek yapın 503-245=? 3 ten 5 çıkmaz onlar basamağına geçeriz, 0 olduğu için yüzler basamağına geçeriz bir tane 100 lük alırız. Geriye dönüşte onlar basamağına aldığımız 100 lükten 90 ını bırakırız yani(9×10) onlar basamağına 9 yazarız sonra kalan 10 u birler basamağında kullanırız. Oda 10+3=13 olur 5 çıkarız 8 kalır, onlar basamağında 9 vardı 9-4=5, yüzler basamağından 1 yüzlük almıştık 5-1=4 kaldıydi 4-2=2 kalır çıkarma işlemini yapınca. Yani sonuç 258 olur. 6 lık tabanda şöyle olur 503-245=? 3 ten 5 çıkmaz soldakı altılar basamağına gidilir 0 olduğu için otuzaltılar basamağına gidilir(36 ve 6’lar basamağı şudur nasılki yüzlük sistemde onlar basamağı 10 üzeri 1 den 10 ve yüzler basamağı 10 üzeri 2 den 10×10=100 ediyorsa, 6 tabanındada 6 üzeri 1 den 6 ve 6 üzeri 2 den 36 eder) ve ordan bir otuz altılık alınır dönüşte 6 lar basamağına 30 u bırakılır ve kalan 6 (10 luk tabanda 10 eklediğimiz ve 90 ı sola bıraktığımız gibi)ilk basamağa eklenir. İlk basamakta 3 vardı 6 ekleyince 9, 245 teki 5 i cıkarınca #4# kalır. 6 lar basamağına 30 verdiydik oda (10 luk tabanda onlar basamağına 90 bırakıp 90\10=9 yazdığımız gibi)30\6=5 ekleriz 5+0=5, 245 teki 4 ü çıkartırız #1# kalır. 36 lar basamağındaki 5 ten 1 ini almıştık 4 kalmıştı 245 teki 2 yi çıkarınca #2# kalır. #İçindeki bulduğumuz rakamlar# ı yazınca sonuç =#214# tür. İnşallah anlatabilmişimdir. Kolay gelsin…
Teşekkürler
72/5 sayısı 5 tabanın da kaçtır? çözüm yolu nasıl bu tarz soruların bilen var mı acaba?
72/5=24 kalan 2dir 2 isaretlenir tekrar 24/5=4 kalan 4 isaretlenir en son =4 5e bolunmeyecegi icin oda isaretlenir cevap isaretlenenler sondan baslanarak yazilir (442)5 tabaninda olur.
Islem hatasi yapmisim bolmede farkinda olmadan cevap (242)5 tabaninda
72/5 sayısını bölüm + kalanı şeklinde yazın. 14 tam + 2.5 şeklinde. 14’ü yaz ayrı 5 tabanında* sonra 2+ 0.5’uda yaz onluk tabanda 0.5 = tabanın sağ tarafına gider (00.1)5 = misal 0.5 kalanlarıda öyle yaz işte topla sonra.
Değerli konu anlatımınız için teşekkür ederim. Tek yanlış sanırım sonda 4 tabanda yazılmış olan 246 sayısının birler ve onlar basamağının 4’e eşit ve büyük olması. Taban aritmetiği sistemine ters düşen bir durum olarak konu girişinde söylendi diye hatırlıyorum.
taban kadar alacaksın yanı 6 kadar alacaksın diğer çıkarma ışlemınden tek farkı bu belk bu şekıl daha ıyı anlarsın
Konu anlatimi gayet açık.Teşekkurler
sağlamasını deneyin kararsızsanız 🙂
Hata yoktur. Bunu 6 lik tabanlari onluk tabana cevirip cikarma islemi yaparak ve tekrar buldugunuz sonucu 6lik tabana cevirerek bulabiliriz… Tşk
503-254=258
Bölme işlemi neden yok?
çıkarma işlemi hatalı
(214) 6 tabanında
2.6^2+1.6^1+4.6^0= 72+6+1=79 tane sayı farketmiştir.
çıkarma işleminde bir hata mı var?
Hata yok.5’den bir 6’lık alınınca 0 rakamı 6 oldu. 3’den 5 çıkmayacağı için bir altılık ona devretti. 3+6=9 oldu. Yani sayı 503’den 459’a dönüştü 🙂
Helal 🙂
gül 5 ten 6 nasıl alıyorsun 6 dan altı istesen veya 7 den anlıycağımda 5in içinde 6 yokkı ?
bak taban 6 olduğu için 6 lık alıyorsun o 5 in yerinde 4 kalıyor ve işlemi öle yapıyorsun çıkarma işleminde yanlışlık yok yanlışlık olsa internete koyarlar mı
taban aritmetigindeki çıkartma işleminde bir yanlışlık yokmu?
Hayır yok